On June 8th 2017, Benjamin Chauvin defended his Ph.D. entitled "Applicability of mechanics-based restoration: boundary conditions, fault network and comparison with a geometrical method".
Congratulations Dr. Chauvin!
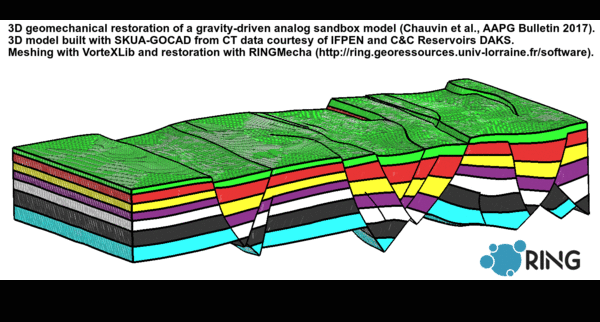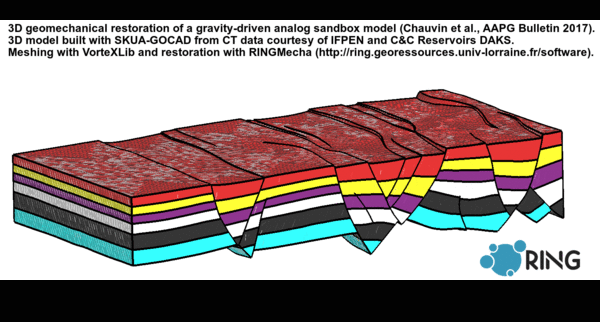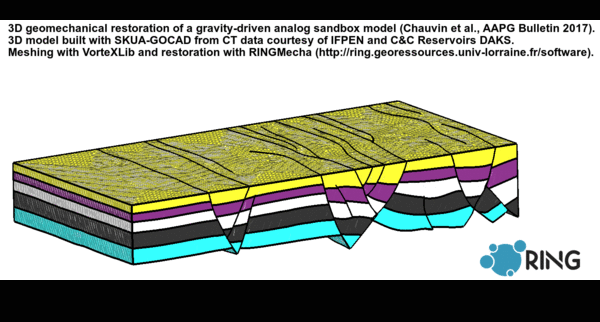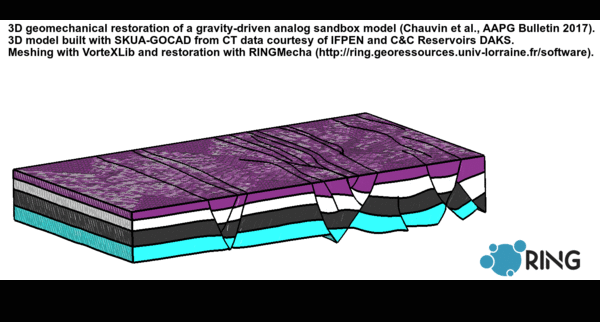
The video of the defense is availalble on YouTube.
Abstract:
Structural restoration aims to recover rock paleo-geometries and to validate structural interpretations. The classical methods are based on geometric/kinematic assumptions and impose a style of deformation. Geomechanical methods, by integrating rock elastic behavior and fundamental mechanical conservation laws, aim to solve issues of classical methods. However several studies show that the geomechanical restoration lacks physical consistency in particular because of the boundary conditions. There are uncertainties on the choice of the elastic properties, and the meshing constraints limit this method to be used as a validation tool of structural interpretations. The choice of a specific restoration method is difficult because there are many geomechanical restoration approaches, in addition to the numerous geometric/kinematic methods. Firstly, this thesis presents a review of the various 3D geomechanical methods to unfold and unfault a 3D geological model. The objective is to present their, theoretical and practical, strengths and limits. Secondly, through the restoration of a structural sandbox model, we worked on the choice of adequate boundary conditions to get a proper restored model. This structural sandbox model was deformed in laboratory and presents several analogies with post-salt extensional structures. Thanks to the observation of the analog model geometry through time on a cross section, we show that a lateral shortening boundary condition is necessary. We show that this shortening can be estimated by the area-depth method. Moreover we define new fault contact conditions to handle complex fault networks. These novel conditions tie internal fault borders and join parts of offset faults. Thirdly, the test of several elastic parameters shows that Young’s modulus, homogeneous within a geological model, has almost no effect on the restoration displacement field. However, Poisson’s ratio has a significant impact on the volume dilatation. Finally, we compare the mechanics-based restoration method with a geometric-based method relying on a chronostratigraphic model (GeoChron) mapping any point of the subsurface to its image in depositional (Wheeler) space. We show that both methods provide a geometrically similar restored state for the analog model. The geometric method has numerous advantages to quickly and accurately get a restored model, but it lacks flexibility on the choice of the deformation constraints. The geomechanical restoration method force is to define custom boundary conditions and specific mechanical behaviors to handle complex contexts.
This Ph.D. was advised by Guillaume Caumon (Univ. Lorraine) and John H. Shaw (Univ. Harvard).
The other members of this Ph.D. committe were: Isabelle Moretti, Delphine Rouby, Jean-Paul Callot, Catherine Homberg, Frantz Marten and Peter Lovely.
This work was implemented in:
This work was funded by ASGA and Chevron. We thank in particular the members of the RING-GOCAD Consortium and Chevron for supporting this research, Paradigm for providing the SKUA-GOCAD software and API, and IFPEN and C&C Reservoirs for providing the computed tomography data set of the structural analog model.
Benjamin is now a Post-Doctoral Fellow in Harvard.
